系統樹のアルゴリズムまとめ
系統樹作成の大きな流れ
①DNAやタンパク質配列をマルチプルアライメント
②マルチプルアライメントの結果に基づき、系統樹を作成する。
という2つのステップがあります。ここでは②のアルゴリズムについて解説します。
系統樹作成のためのアルゴリズム
系統樹作成のためのアルゴリズムは、大きく分けて背後にある祖先の配列を考慮する方法(文字列置換利用法)としない方法(距離行列法)に区分されます。
一般に、文字列置換利用法の方が計算時間はかかるものの正確な系統樹が得られるという特徴があります。
実際のアルゴリズムとしては以下のようなものがあります。
| 分類 | 方法(名称) | 説明 |
|---|---|---|
| 距離結合法 | UPGMA法 | 距離的に一番近いものからまとめていく手法。進化速度が一定である仮定をおいている。 |
| 近隣結合法(Neighbor-Joining: NJ法) | できるだけ少ない進化事象で進化の履歴を説明する系統樹を求める方法。星型系統樹からはじめ、枝の長さの総和を最小にする対を順々にくくりだす。 | |
| 文字置換利用法 | 最大節約法(maximum parsimony: MP法) | 全通りの樹を考え、その中で塩基の置換回数が少ない樹形を導く方法。 |
| 最尤法(Maximum Liklihood: ML)法 | 塩基置換に関してモデルを仮定し、そのモデルに基づき尤度(確率)の高い樹形を導く方法。 |
# UPGMA法のアルゴリズムと計算例
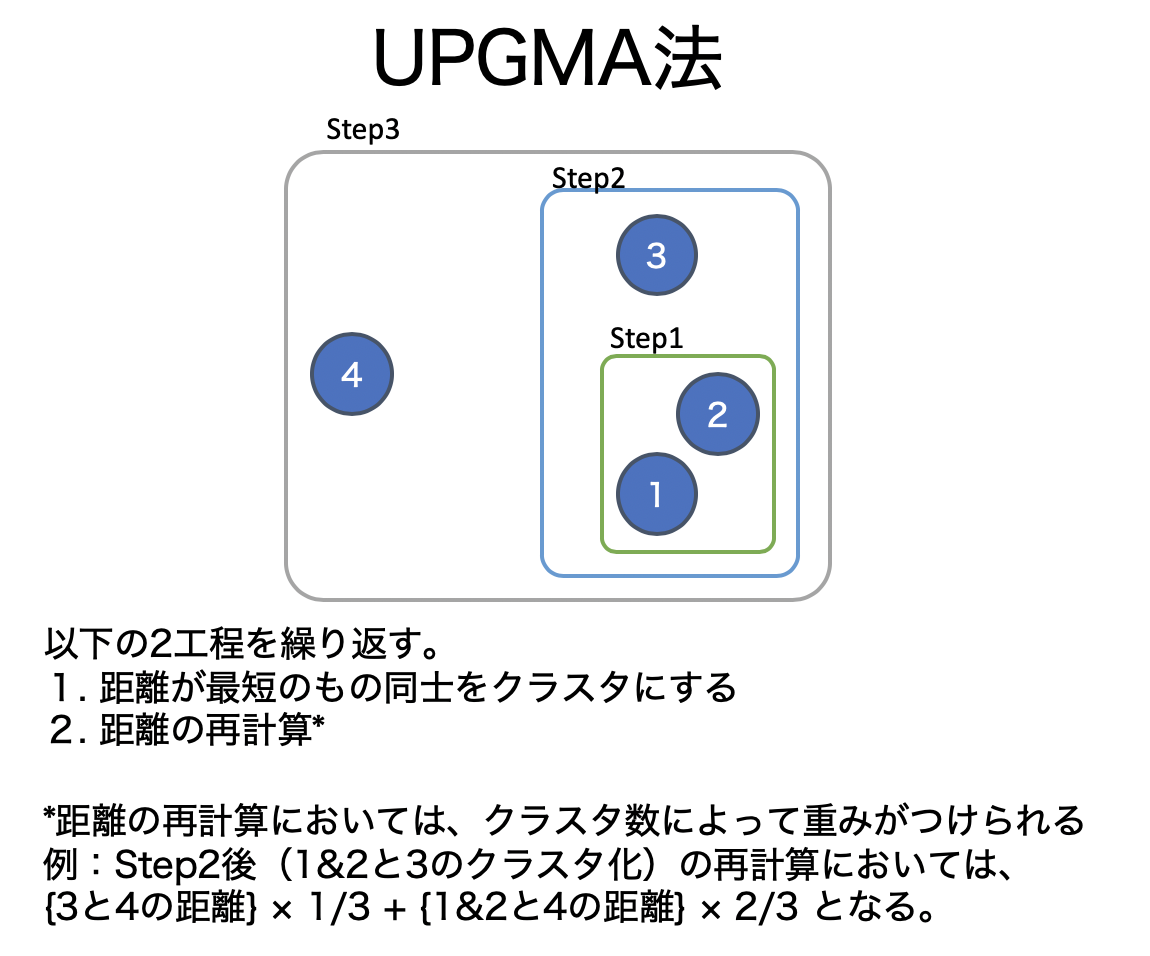
(図は神嶌先生のページを元に作図)
「距離が最短のもの同士をクラスタにする」と「距離の再計算」の2工程を繰り返す手法。
距離の再計算においてはクラスタ数によって重み付けされる。
# 近隣結合法(NJ法)のアルゴリズムと計算例
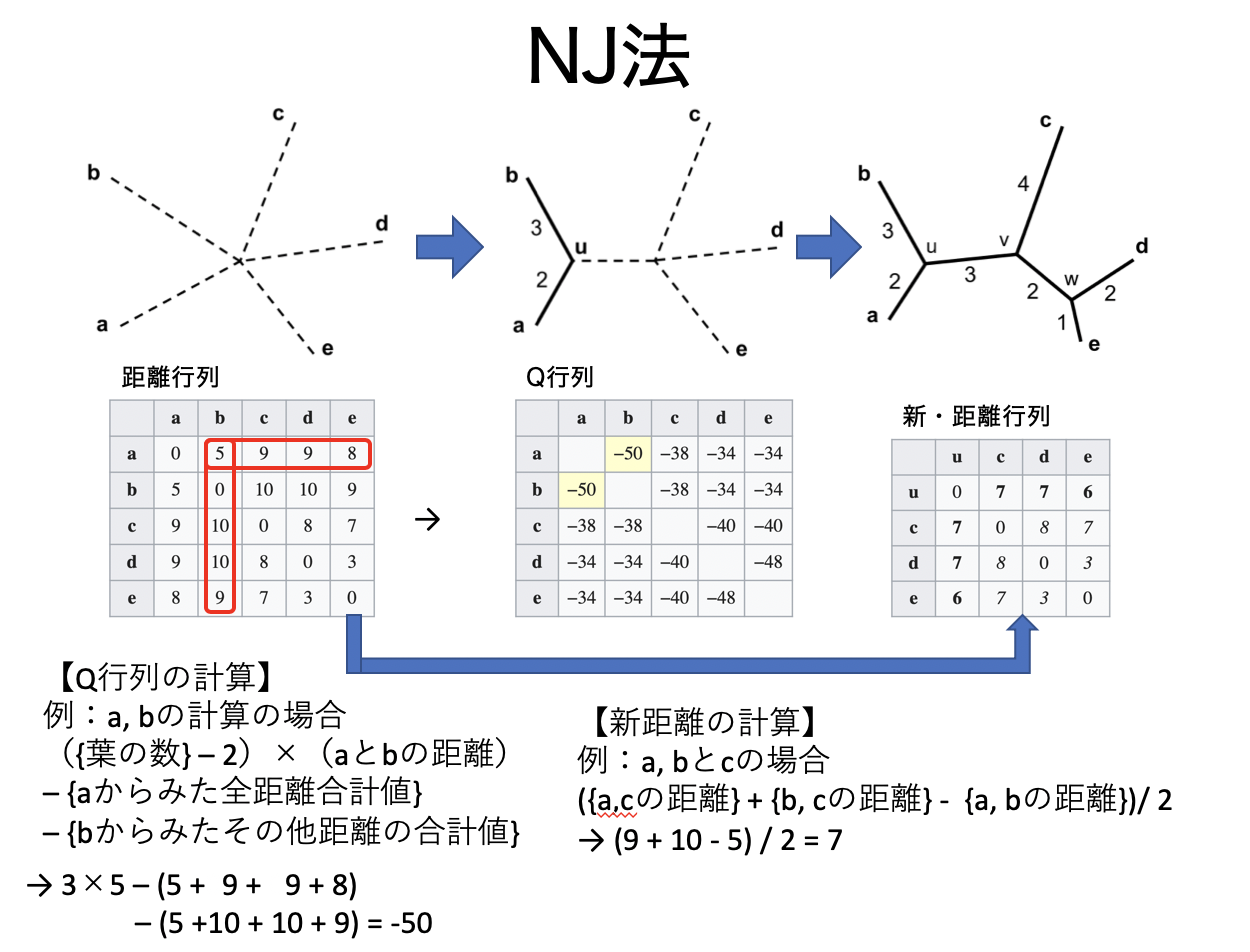
こちらもクラスタ化→距離の再計算を繰り返すのみだが、
クラスタ化のときに「距離が短く、他との距離が離れているもの」をクラスタ化する特徴がある。
# 最大節約法(MP法)のアルゴリズムと計算例
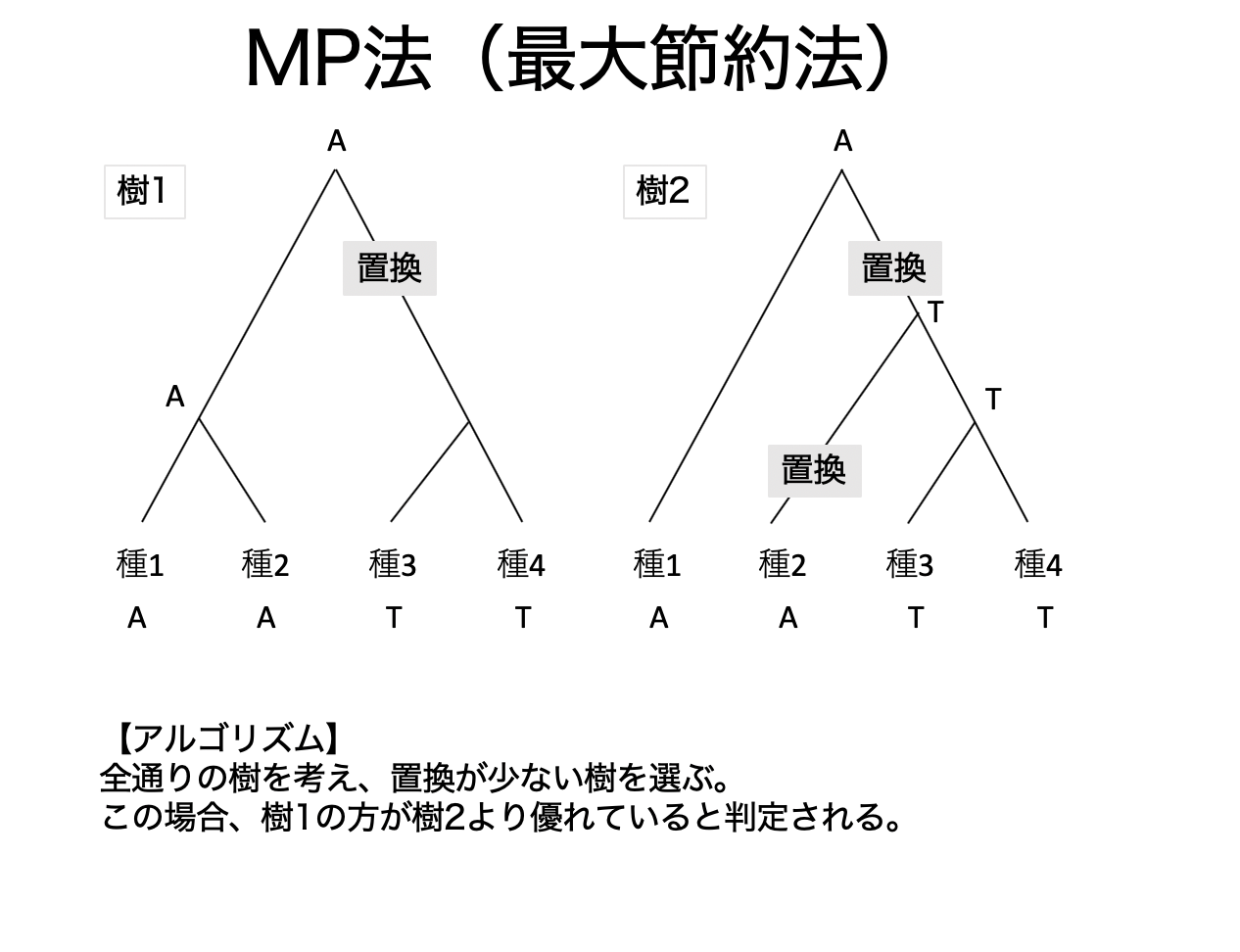
画像は川端先生のページを元に作成4
全通りの樹を考え、その中で塩基の置換回数が少ない樹形を導く方法。
同じ部位で複数回置換が起きること(多重置換)を考慮していないため、遠縁な配列同士の系統樹の作成には向いていない。
# 最尤法(ML法)のアルゴリズム

全通りの樹を考え、その中で確率(尤度)が高い樹形を導く方法。
塩基やアミノ酸の置換については、既報の報告(Jukes-Cantorモデル,Kimura2パラメータモデルなど)を使用する。
また、上記尤度をMCMC法によって求めるベイズ法なども近年報告されています。5
まとめとどのアルゴリズムを用いるべきか?
業界や近辺の論文の常識に従うのが一番ですが、
枝の数が多い場合、計算時間の都合上、距離行列法を使うこととなります。
枝の数が少ない場合は最尤法やベイズ法を使うとよい樹が得られることが多いです。